Die Mitternachtsformel: Ein Schlüssel zur Lösung quadratischer Gleichungen
Die Mitternachtsformel, auch bekannt als „abc-Formel“ oder „quadratische Lösungsformel“, ist ein zentrales Werkzeug in der Mathematik, insbesondere im Schulunterricht. Sie ist essenziell für das Lösen von quadratischen Gleichungen, also Gleichungen der Form ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0. Mit Hilfe der Mitternachtsformel können die Lösungen solcher Gleichungen schnell und effizient gefunden werden, was sie zu einem unverzichtbaren Bestandteil mathematischer Grundkenntnisse macht. Doch was genau steckt hinter dieser Formel, warum ist sie so wichtig, und woher stammt der ungewöhnliche Name „Mitternachtsformel“.
Mittelnachtsformel Rechner
Mitternachtsformel Rechner
Die Herleitung der Mitternachtsformel
Um die Mitternachtsformel zu verstehen, ist es hilfreich, die Schritte zu kennen, die zu ihrer Herleitung führen. Ausgangspunkt ist die allgemeine Form einer quadratischen Gleichung:
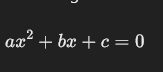
Das Ziel ist es, die Werte für xxx zu finden, die diese Gleichung erfüllen. Ein allgemeiner Ansatz besteht darin, die Gleichung zu faktorisieren, was jedoch nicht immer einfach oder möglich ist. Deshalb wird stattdessen oft der Ansatz des „Vollständigen Quadrats“ verwendet, um die Gleichung umzuformen.
Zunächst teilt man die gesamte Gleichung durch den Koeffizienten aaa (vorausgesetzt, aaa ist nicht null):
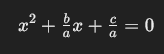
Dann wird die Gleichung so umgeformt, dass auf der linken Seite ein vollständiges Quadrat entsteht. Dazu addiert und subtrahiert man den Term (siehe Bild unten).
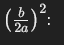
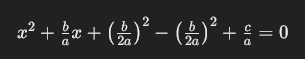
Dieser Ausdruck kann umgeschrieben werden als:
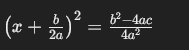
Indem man auf beiden Seiten die Wurzel zieht und den Bruch vereinfacht, erhält man:
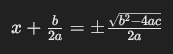
Durch Subtraktion von
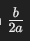
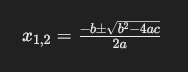
Tipp: Mehr über Bildung
Die Diskriminante: Ein Indikator für die Art der Lösungen
Ein entscheidendes Element der Mitternachtsformel ist die Diskriminante, Δ=b2−4ac\Delta = b^2 – 4acΔ=b2−4ac, die sich unter der Quadratwurzel befindet. Die Diskriminante gibt Aufschluss darüber, wie viele Lösungen die quadratische Gleichung hat und welche Art diese Lösungen annehmen:
- Δ>0\Delta > 0Δ>0: Die Gleichung hat zwei reelle und unterschiedliche Lösungen. Dies ist der Fall, wenn die Diskriminante positiv ist. Die beiden Lösungen können durch die Mitternachtsformel direkt berechnet werden.
- Δ=0\Delta = 0Δ=0: Die Gleichung hat genau eine reelle Lösung, auch als doppelte Nullstelle bezeichnet. Diese Situation tritt auf, wenn die Diskriminante null ist, was bedeutet, dass die Parabel die x-Achse berührt, aber nicht schneidet.
- Δ<0\Delta < 0Δ<0: Die Gleichung hat keine reellen Lösungen, sondern zwei komplexe Konjugierten. Dies tritt auf, wenn die Diskriminante negativ ist. In diesem Fall existieren keine Schnittpunkte mit der x-Achse im reellen Zahlenbereich.
Die Diskriminante spielt somit eine zentrale Rolle, da sie es ermöglicht, bereits vor der Berechnung zu verstehen, welche Art von Lösungen man erwarten kann.
Anwendung der Mitternachtsformel in verschiedenen Bereichen
Die Mitternachtsformel findet in vielen Bereichen Anwendung, die über die reine Mathematik hinausgehen. Hier einige Beispiele:
Computerwissenschaften: Auch in der Informatik findet die Mitternachtsformel Anwendung, beispielsweise bei der Implementierung von Algorithmen zur Berechnung von Nullstellen in numerischen Methoden.
Physik: In der Physik tritt die Mitternachtsformel oft auf, wenn es um die Bewegung von Objekten unter Einfluss von Kräften geht. Zum Beispiel bei der Berechnung von Wurfparabeln oder der Bestimmung der Reichweite eines Projektils.
Ingenieurwissenschaften: In der Technik und Ingenieurwissenschaften wird die Mitternachtsformel verwendet, um Optimierungsprobleme zu lösen. Beispielsweise bei der Auslegung von Tragwerken oder der Analyse von Schwingungen.
Ökonomie: In der Wirtschaftsmathematik kommt die Mitternachtsformel bei der Berechnung von optimalen Produktionsmengen, Preisbildung und bei der Bestimmung von Gewinnmaximierungen zum Einsatz.
Fazit
Die Mitternachtsformel ist ein kraftvolles Werkzeug, das aus der Mathematik nicht wegzudenken ist. Sie ermöglicht das einfache Lösen quadratischer Gleichungen und bietet durch die Diskriminante wertvolle Informationen über die Art der Lösungen. Von der Physik bis zur Informatik, die Mitternachtsformel ist universell einsetzbar und bleibt ein Grundpfeiler mathematischer Bildung. Ihr Name, der darauf hindeutet, dass man sie zu jeder Tages- und Nachtzeit auswendig beherrschen sollte, ist dabei ebenso einprägsam wie die Formel selbst.

